隕石はどこまで見えますか?
>メールが届きます。
ほとんどはさまざまなタイプの質問をしており、そのほとんどは答えるのがかなり簡単です(実際、多くはグーグル、ヒントヒントによって答えることができます)。しかし、答えるのが難しい質問や、自分自身について疑問に思っていたのに理解できなかった質問を受け取ることがあります。
ですから、バッドリーダーのディーンルイスから流星について質問を受けたとき、私はかなり興味をそそられました。 2018年のペルセウス座流星群の間、彼は家族から離れていて、約1,000キロメートル離れていました。もし彼が隕石を見たとしたら、彼らはもっと遠い場所から同じ隕石を見ることができたのでしょうか?
簡単な答えは:はい!長い答えは…数学です。かっこいい、楽しい数学。
そして、この記事が投稿されたとき、2018年のふたご座流星群が今夜どのようにピークに達するかを考えると、これを理解するのが適切だと思います。
ドローン読書レベルの秘密
クラッシュコース天文学:流星、流星物質、隕石、オーマイ!
地球が完全に平らである場合、原則として、地球のどの端までも隕石を見ることができます。あなたが地上にいる限り、たとえほんの少しでも、あなたの視線はあなたの側の惑星のすべての平方センチメートルに達するので、すべての流星は誰にでも見えるようになります。実際には、空気は完全に透明ではないため、ある距離では、何も見えないほど多くの泥を眺めています。
しかし、地球は平らではありません。真剣に!丸いです。そして、大気はそれを貝殻のように取り囲み、高さとともに薄くなり、最終的にはペタリングします。その高さは、スペースの定義によって異なります。しかし、私たちは科学を知っているので少しごまかすことができます。シャワーのような流星は、地上約100kmで燃え尽きる傾向があります。その高さは、その大きさなど、多くのことに依存します 流星物質 (惑星間破片が宇宙を飛び回る固体の断片)は、それらがどれだけ速く動いているか、それらが大気に入る角度などです。しかし、それを100kmと呼びましょう。
隕石があなたに最も近いのは、隕石の真下にいて、100 km真上(天頂)にある場合です。それが天頂から遠く離れて燃え尽きるなら、それはあなたから遠く離れているに違いありません。隕石を見ることができる最も遠いところにあるのは当然のことです。したがって、それがまさに地平線上にあるかどうかです。
その形状は次のようになります(注:縮尺どおりではありません):
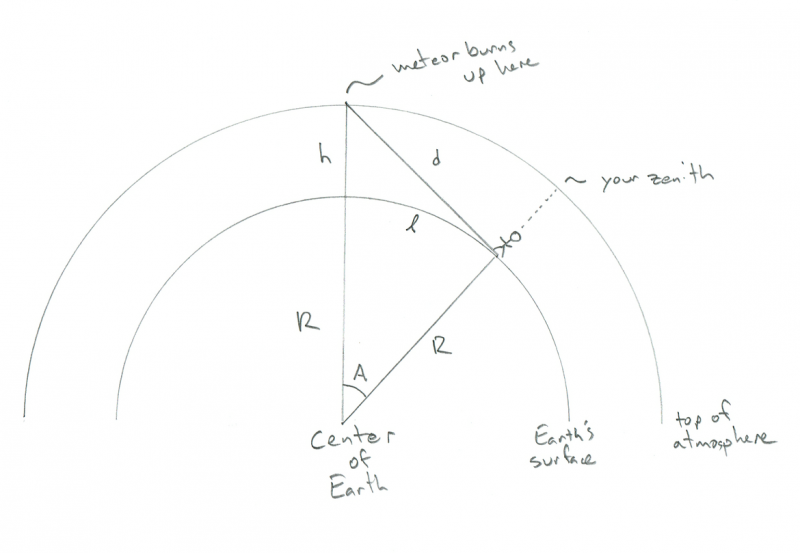
隕石が燃え上がるのを見ている観測者の幾何学を示す概略図。クレジット:Phil Plait
湾曲した地球の表面に人間が立っている小さな棒人間を見ることができます—たとえばあなたです—その上に(これも湾曲した)大気があります。この図では、Rは地球の半径(6,4000 km)、hは流星が燃え尽きる高さ(100 km)、dはあなたから流星までの距離です。 Aは地球上の自分の位置とその上の隕石の位置の間の角度であり、筆記体l(長さなど)は隕石を真上に置くために歩く必要がある距離です(奇妙なことのように思えます)知りたいが、我慢して)。奇妙なことに、dを知らなくても、ここで必要なすべてを計算できますが、流星がどれだけ離れているかを知るのはクールですよね?
これらすべての鍵は、流星、あなた、そして地球の中心の間の角度が直角であることを確認することです。これは、流星があなたから見た地平線上にあるためです(または、楽しい専門用語が必要な場合は、Rが交差する内側の円の接線上にあります)。これにより、三角形は直角三角形になります。高校の数学を覚えていれば、すべての辺と角度を見つけることができます。
覚えて ピタゴラスの定理 ?直角三角形では、斜辺の長さの2乗は、他の2つの辺の2乗の合計に等しくなります。*。私たちの三角形では、hypotenuseはR + hであり、他の辺はRとdです。
それで
(R + h)2= d2+ R2
または、左側を乗算します(を使用します ホイル ):
NS2+ 2Rh + h2 = d2+ R2
dを解いて、流星があなたからどれだけ離れているかを確認します。 R2は両側にあるので、キャンセルして取得することに注意してください
NS2= 2Rh + h2
または
d =平方根(2Rh + h2)
まあ、私たちはそれらすべての数字を知っています!プラグアンドチャグ、赤ちゃん:
d =平方根(2 x 6,400 x 100 + 10,000)= 1,136 km
あはは!これは、地平線上に隕石が見える場合、それは1,100km以上離れていることを意味します。それは長い道のりであり、技術的には、地面から隕石を見ることができる最も遠い場所です。
それでは筆記体lを見つけましょう。まず、角度Aを知る必要があります。これには三角法が必要です。たくさんある トリガーID あなたはこれを理解するために使うことができますが、私のお気に入り†直角三角形では、角度の正弦は反対側の長さを斜辺の長さで割ったものです。したがって、その比率を取得すると、逆正弦(またはアークサイン)を使用して角度を取得できます。
sin(A)= d /(R + h)
それで
A =なし-1(d / R + h)
もう一度プラグアンドチャグすると、A = 10°になります。それは地球の表面のまともな塊です!
そして今、筆記体lを取得できます。地球の周りには360°があり、地球の円周は2 x pix半径= 40,192 kmなので、
40,192 km / 360°= 1度あたり112キロメートル
つまり、10°= 1,120キロメートルになります。これはdにかなり近いですが、それほど驚くことではありません。図面は誇張されていますが、実際には私たちの上の空気の殻は地球のサイズに比べて小さいです。縮尺どおりに図面を作成した場合、dとlの長さが実際にかなり近いことがわかります。
さて、なぜ私はみんな熱くて、lを見つけるのに悩んでいるのですか?元の質問のために!その計算をすべて忘れた場合、2人がどれだけ離れていても、同じ流星を見ることができるでしょうか。
その場合、流星はそれらの間に直接あり、それぞれの地平線上にあります。そのジオメトリは次のようになります。
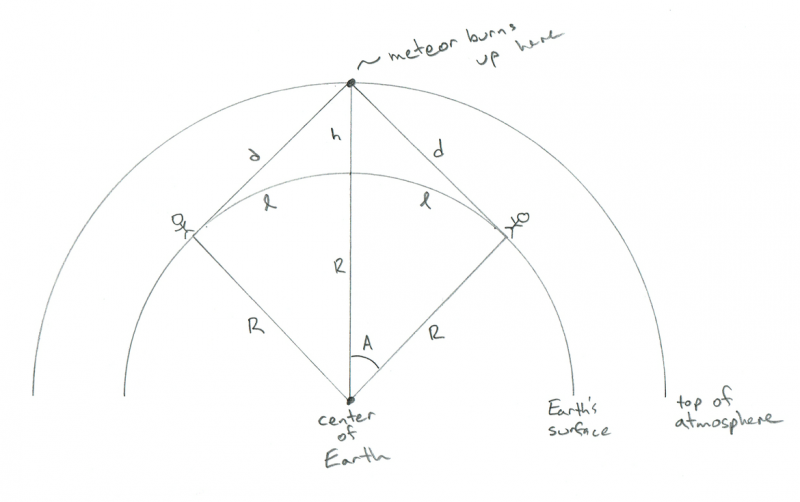
隕石がちょうどそれらの間で燃え上がるのを見ている2人の観察者の幾何学を示す概略図。クレジット:Phil Plait
AHA!今、あなたは私がなぜlが欲しいのかわかります!二人の距離はたったの2×l!だから今、私たちは答えを持っています:
シェイプ・オブ・ウォーターの親ガイド
2人が同じ流星を見るには、2 x 1,120 = 2,240キロメートルしか離れていません。例として、それはワシントンDCとデンバーの間の距離にかなり近いです。わお。
ちなみに、(文字通り)視点を変えると、これは流星の視点から、幅2,240 kmの地球の広がりを見ることができることを意味します(地球の東端のDCと西端のデンバーのように)。それはいいね。
そして、それはディーンの質問に対する実際の答えに私たちをもたらします:彼が彼の家族から1,000 km離れていれば、そうです、技術的には彼らは同じ流星を見ることができました。どのようにそのことについて?
さて、これもまた、空気が完全に澄んでいて、実際には本質的に不可能であると仮定しています。したがって、この数学は理想的な状況を表しています(流星が正確にそれらの間にあるという考えを含む)。
もっと現実的にしましょう。両方の観測者にとって、流星が地平線から45°の高度で空に燃え上がったとしましょう。それらは互いにどれくらい離れているでしょうか?さて、再び流星が正確にそれらの間にあると仮定すると、ジオメトリは次のようになります。
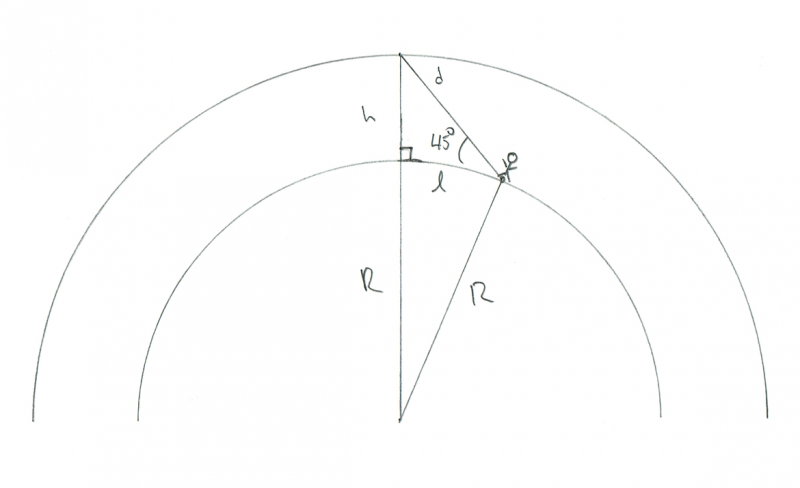
地平線から45°上で燃え上がる流星を見ている観測者の幾何学を示す概略図。クレジット:Phil Plait
これは実際には解決が難しいですが、別のトリックを知っています。lが小さいと仮定すると、地球の曲率は重要ではなくなります。たとえば、庭にある2本の木の間の距離を知りたい場合、地球が曲がっていてもかまいません。こんなに短い距離では、平らだと思います。ここでその仮定をしましょう。
その場合、別の直角三角形がありますが、今回は直角が流星の下の角度です。私はそれを図の中で小さな四角い記譜法でラベル付けしました。したがって、それが90度の角度で、流星に対する角度が45度の場合、最後の角度(流星から観測者まで)も45度になります。つまり、これは二等辺三角形でなければならないので、lとhは同じです! hが100kmであることがわかっているので、lも必要です。
つまり、2人の観測者間の距離はその2倍、つまり200kmです。
ちなみに、この場合、流星までの距離は約141kmです。読者への演習として、それを確認しておきます。
原則として、これは、隕石が地平線からどれだけ高いか、そして隕石が燃え上がった高度がわかっている場合、その距離を計算できることを意味します(または、距離がわかっている場合は、その高さを取得できます)。ただし、そのトリガーはかなり複雑であり、今日は十分な計算を行ったと思います。
しかし、高校の数学のほんの少しがとても楽しいアプリケーションを持つことができると考えるのはクールです。そして、分離がそれほど遠くない限り、流れ星を見ることを他の誰かと共有することが可能であることを知っていることは詩的でロマンチックであることを認めます。なんて素敵な考えでしょう。
* の オズの魔法使い 、かかしはこれを間違えました 後 彼は頭脳を得た。
† の コース 私は好きな三角法のアイデンティティを持っています。君は?